The concurrent activation of two or more muscles.Co-activation can be observed between combinations of agonist, synergist and/or antagonist muscles about a joint. During agonist–antagonist co-activation, the resultant moment of the force is lower than the individual contributions from agonist and antagonist muscles and there is an increase in the mechanical impedance (i.e., resistance to motion) of the joint (beyond what would be expected for similar net moments generated in the absence of co-activation).

Indicator of the linear relationship or dependency between two random (stochastic) processes as a function of frequency (or time and frequency), measured on a scale from 0 to 1 (0 means the processes are uncorrelated, and 1 indicates a perfect linear relationship). The coherence (or magnitude-squared coherence), C_xy(f), indicates how much each component of the spectrum of x is related to the same frequency component of the spectrum of y, as reported in Formula 1. S_xy(f) is the cross-power spectral density between signal x and signal y, and S_xx(f) and S_yy(f) are the auto-power spectral densities of signals x and y, respectively. When the coherence between two signals is < 1, it indicates that there is some independent component contained in one of the signals that is not present in the other and/or there is a nonlinear relationship between the two signals.

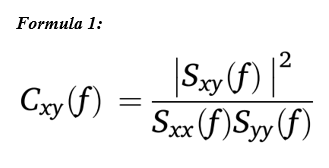
The ratio of the differential gain of an amplifier (A_d) to the common mode gain (A_cm). It quantifies the ability of an amplifier to reject common-mode signals (unwanted signals seen at both input terminals) and amplify differential signals (signals that are different at the input terminals). The ratio is usually measured in decibels (dB). CMRR = 20 Log 10 |A_d/A_cm|. An ideal amplifier would reject all common-mode signals, i.e., CMRR would be infinite.

The continuous wavelet transform is one of many time-frequency representations used in signal processing. These transforms deconstruct a time-domain signal into a sum of “wavelets” of different scales and time shifts, to produce a time-frequency representation of a time-domain signal. It is often applied to signals that exhibit temporal variations in frequency content (i.e., non-stationary signals). The continuous wavelet transform, CWT_x, of a signal x is given by the convolution of the signal with a wavelet function, Ψ, as per Formula 1. The * denotes the complex conjugate and Ψ is a function of s and τ, where s is the resolution or scale factor, τ is the time shift factor and t is time. The wavelet function is stretched or compressed by changing the scale factor. In contrast to the Fourier expansion, the basic waveforms into which the signal is decomposed are not sinusoids but finite duration waveforms that are concentrated in time. There is a variety of such waveforms with different properties.

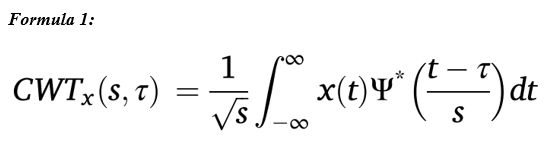
Estimate of the linear relation between two signals (or between two series of samples) as a function of the time displacement of one relative to the other. The cross-correlation function, Rxy, of two finite, discrete signals, x and y, can be estimated as per Formula 1. N is the total number of samples in the signal, m is the lag in samples (i.e., m = 0, ±1, ±2, …, ±(M−1), M is the range of lag values where M ≪ N) and xn and yn are the values of the nth samples within the signals x and y, respectively. This is a biased estimate of R_xy, but the bias is small where M ≪ N. Cross-correlation can be used to estimate the delay between similar or identical signals (e.g., for the estimation of conduction velocity). For example, if y(t) = x(t−τ), the cross-correlation function between x(t) and y(t) is equal to 1 for the time delay τ, i.e., y(t) is a time-delayed version of x(t) and the time delay is τ seconds. The equation for R_xy in continuous time can also be expressed as (note that below we provide the expression over the entire time axis) in Formula 2. The cross-power spectrum of signals x(t) and y(t) can be obtained by taking the Fourier transform of their cross-correlation, R_xy.

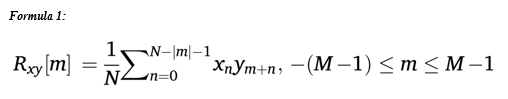
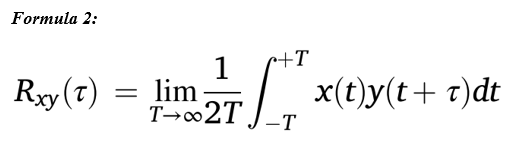
EMG signals from muscles other than the muscle of interest. Crosstalk from surrounding muscles can be detected when recording from small or thin muscles, when muscles are interposed between the muscle of interest and the electrode, or when using electrodes with a large inter-electrode distance due to their large detection volume. Crosstalk is an important consideration for study design and electrode selection (Besomi et al, 2019).

The rate of flow of charged particles per unit time (Coulombs per second, C/s, or Amperes, A). 1C = 6.25 × 10¹⁸ electrons.